

The accuracy of the wave function-based methods in Quantum Chemistry is evidently dependent on both the reliability of the method employed and quality of the basis set that limits the accuracy.
Ideally, a chosen finite basis set should reproduce the complete basis set (CBS) limit. However, in real life, to approach the CBS limit one needs to employ very large finite basis sets and their practical use is currently limited to fairly small molecular systems.
Attempts to address the CBS limit problem have led to the emergence of a wide variety of the extrapolation schemes [1-9] where the infinite basis set calculations are realized by extrapolation to the CBS limit. These extrapolations are often based on formulas for the asymptotic convergence of energies and other properties to their CBS limit. Many of such extrapolation schemes use two- or three-point extrapolation formulas, with each point being obtained with the progressively larger basis set. Good examples of such basis sets, that are well defined with respect to increasing in both size and accuracy, and that systematically converge towards the CBS limit, are the correlation-consistent basis sets of Dunning [10] and the polarization consistent basis sets developed by Jensen [11].
Though many of extrapolation formulas look simple and represent exponential, Gaussian and power functions, obtaining parameters for the CBS limit extrapolation may be a laborious computational task. This CBS Limit Extrapolation Calculator considerably facilitates calculations of parameters and extrapolated properties.
Halkier et al. [2] found out that an exponential form
(1) |
shows better than a power form (see below) results for the extrapolations to the basis-set limit of the correlation energies. Here X is two for double-zeta sets, three for triple-zeta sets, etc. E∞ is energy at the basis-set limit, and B and α are fitting parameters.
To calculate E∞, B and α analytically for three calculations in (aug-)cc-pVDZ, (aug-)cc-pVTZ, and (aug-)cc-pVQZ basis sets we need to solve a system of equations:
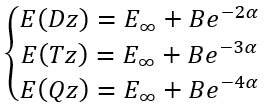 |
(2) |
So, we have
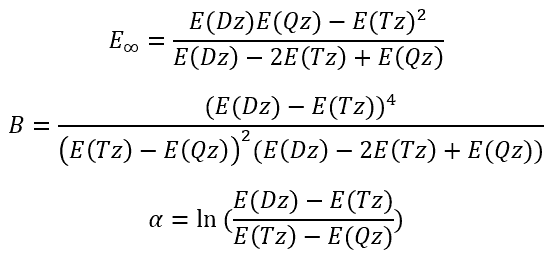 |
(3)
(4)
(5)
|
To calculate E∞, B and α analytically for three calculations in (aug-)cc-pVTZ, (aug-)cc-pVQZ, and (aug-)cc-pV5Z basis sets we need to solve a system of equations:
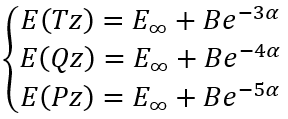 |
(6) |
So, we have
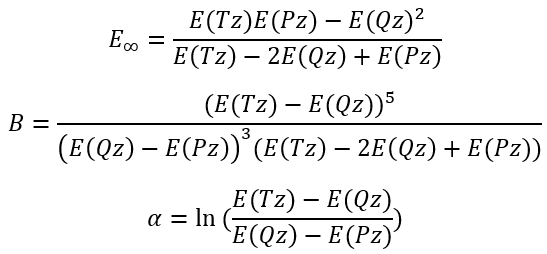 |
(7)
(8)
(9) |
In this case we have a system of equations:
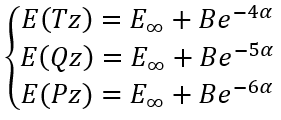 |
(10) |
So, we have the solutions:
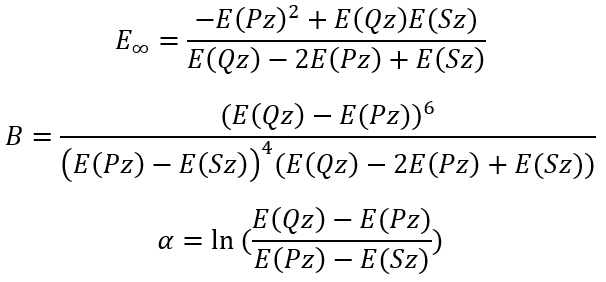 |
(11)
(12)
(13) |
In the case of arbitrary "cardinal numbers" n1, n2, and n3 which can in general case be integer or fractional numbers we have a system of equations:
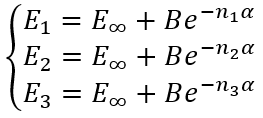 |
(14) |
by defining
(15) |
We need to solve numerically an equation for Z (using, for example, a fixed point iteration method):
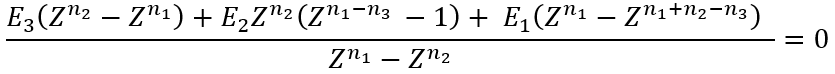 |
(16) |
then we can easily calculate α, B and E∞
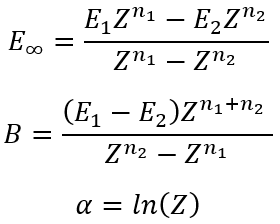 |
(17)
(18)
(19) |
Helgaker et al. [1] found out that a power function in the form
(20) |
where X is two for double-zeta sets, three for triple-zeta sets, etc. can be useful for the extrapolations to the basis-set limit of the correlation energies. E∞ is energy at the basis-set limit.
For the cardinal numbers 2, 3, and 4 we can write a system of equations:
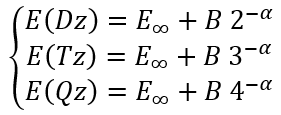 |
(21) |
where E(Dz), E(Tz), and E(Qz) are energies calculated using (aug)-cc-pVDZ, (aug)-cc-pVTZ, and (aug)-cc-pVQZ basis sets, respectively.
Since we cannot solve it analytically we need first to solve numerically an equation (using, for example, a fixed point iteration method):
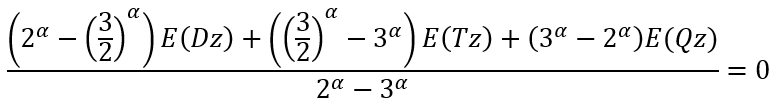 |
(22) |
then we can easily calculate B and E∞:
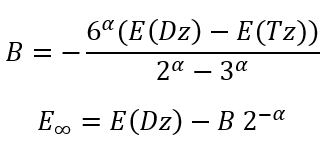 |
(23)
(24) |
For the cardinal numbers 3, 4, and 5 we can write a system of equations:
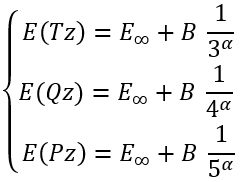 |
(25) |
where E(Tz), E(Qz), and E(Pz) are energies calculated using (aug)-cc-pVTZ, (aug)-cc-pVQZ, and (aug)-cc-pV5Z basis sets, respectively.
Since we cannot solve it analytically we need first to solve numerically an equation (using, for example, a fixed point iteration method):
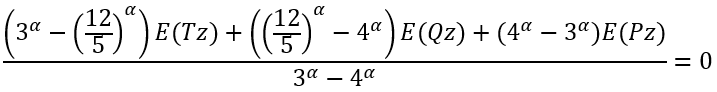 |
(26) |
then we can easily calculate B and E∞:
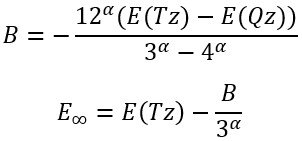 |
(27)
(28) |
In the case of arbitrary "cardinal numbers" n1, n2, and n3 which can in general case be integer or fractional numbers we have a system of equations:
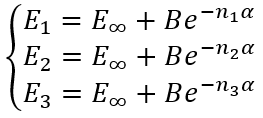 |
(29) |
by defining
(30) |
We need to solve numerically an equation for Z (using, for example, a fixed point iteration method):
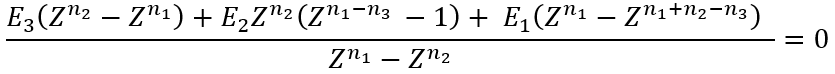 |
(31) |
then we can easily calculate α, B and E∞
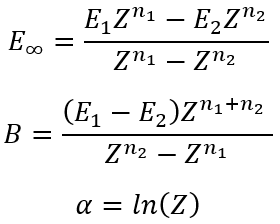 |
(32)
(33)
(34) |
Shortly after the appearance of the exponential extrapolation formula, a three parameter, mixed Gaussian/exponential expression, was suggested by Peterson et al. in the context of a multireference configuration interaction study of the H + H2 → H2+ H exchange reaction [3]. The same expression was used by Woon and Dunning in a paper on first row/second row AB diatomics with various levels of perturbation theory and CCSD(T) [4]. It was noted that the mixed formula fit the total energies through cc-pV5Z better than the straight exponential function. It was also used in other works [5].
A mixed Gaussian/exponential scheme has a form:
(35) |
In the case of arbitrary "cardinal numbers" n1, n2, and n3 which can in general case be integer or fractional numbers we have a system of equations:
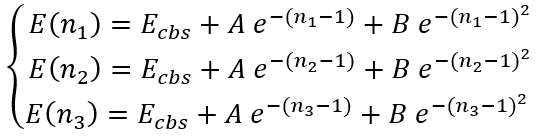 |
(36) |
By solving this system we have an expression for Ecbs:
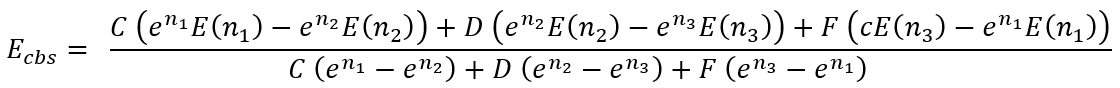 |
(37) |
where
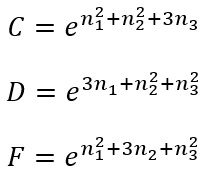 |
(38)
(39)
(40) |
For some particular values of cardinal numbers n1, n2, and n3 the expressions for Ecbs(n1,n2,n3) are presented below:
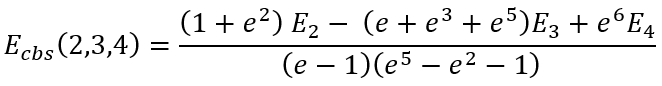 |
(41) |
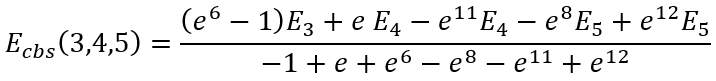 |
(42) |
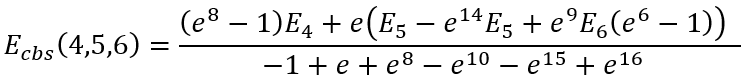 |
(43) |
This scheme was motivated by the 1/Z second order perturbation theory work of Schwartz, who analyzed the correlation energy in 2-electron, He-like systems [6, 7]. Martin [8] considered several approximation formulas.
The first approximation was based on a function:
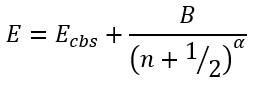 |
(44) |
In the case of arbitrary "cardinal numbers" n1, n2, and n3 which can in general case be integer or fractional numbers and corresponding energies E1, E2, and E3 we have a system of equations:
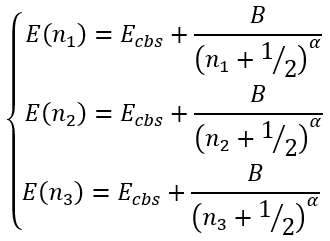 |
(45) |
Since we cannot solve it analytically we need first to solve numerically an equation for α (using, for example, a fixed point iteration method):
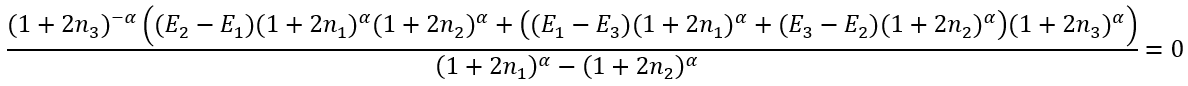 |
(46) |
Then we can easily calculate Ecbs and B:
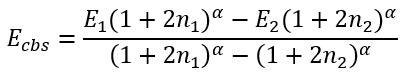 |
(47) |
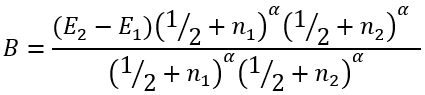 |
(48) |
The next extrapolation of the form
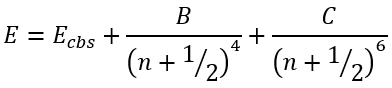 |
(49) |
was found [8] to yield the total CCSD(T) atomization energies (TAEs) accurate, on average, to 0.5 kcal/mol using at most [sdpfg] basis sets. Using [spdfgh] basis sets and a small additivity correction for triple bonds, this can be reduced to 0.2 kcal/mol.
In this case we have a system of equation:
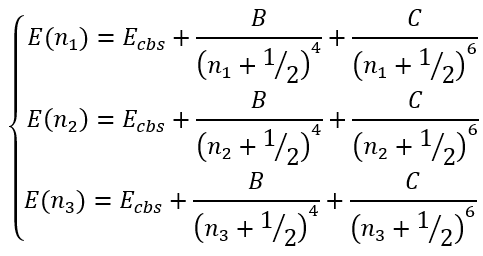 |
(50) |
This system of equations has analytical (though lengthy) solution for Ecbs:
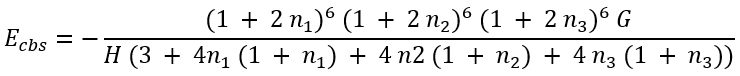 |
(51) |
where
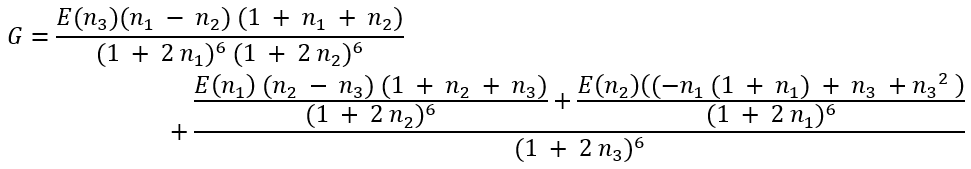 |
(51a) |
and
(51b) |
Knowing Ecbs we can easily calculate B and C:
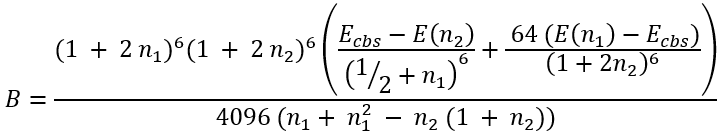 |
(52) |
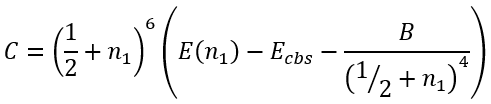 |
(53) |
For some particular values of cardinal numbers n1, n2, and n3 the expressions for Ecbs(n1,n2,n3) are presented below:
 |
(54)
(55)
(56) |
Martin [8] also adopted two parameters expression with the integer exponent:
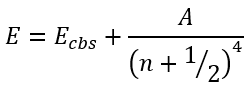 |
(57) |
In this case we have a system of equations:
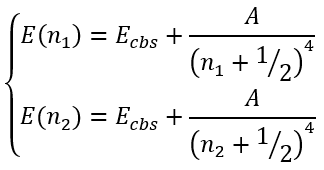 |
(58) |
This system of equations has analytical solution for Ecbs:
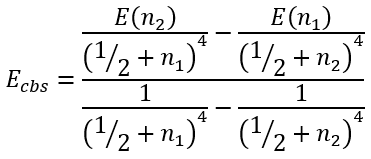 |
(59) |
and
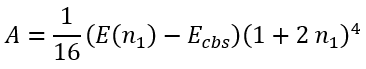 |
(60) |
For some particular values of cardinal numbers n1 and n2 the expressions for Ecbs(n1,n2) are presented below:
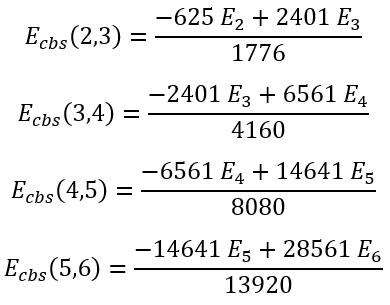 |
(61)
(62)
(63)
(64) |
The next formula involving the inverse power of n was originally presented in a paper discussing the basis set convergence of the water molecule by Helgaker et al. [1]:
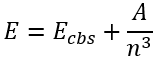 |
(65) |
A year later, a follow-up paper [9] on Ne, N2, and H2O compared the effectiveness of above formula with quintuple and sextuple zeta quality basis sets to explicitly correlated R12 MP2, CCSD, and CCSD(T) calculations.
In this case we have a system of equations:
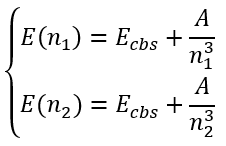 |
(66) |
This system of equations has analytical solution for Ecbs and A:
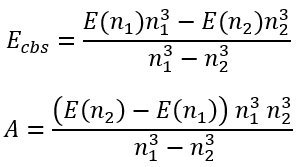 |
(67)
(68) |
A total energy, ETot can be written as
![]()
Where EHF is a Hartree–Fock (HF) energy and Ecorr is a correlation energy. Since the rate of convergence of the correlation part is known to be significantly slower than that of the Hartree–Fock part, different approximation methods are used for the HF and correlation energies.
Authors of [12] considered the total multireference configuration interaction (MRCI) energy split as
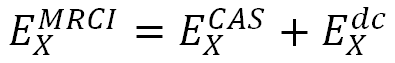
where ECAS is the CASSCF energy and Edc is the dynamical correlation component. Such a partitioning was indispensable to perform good-quality extrapolations, since the CASSCF and dynamical correlation energies had been known to converge with distinct rates for the same number of functions in the basis set [12].
As for the ECAS they used a form:
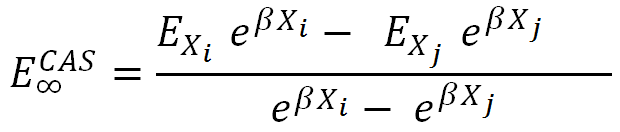
where β is a universal parameter and Xi and Xj are so-called hierarchical numbers which are closely related to the cardinal numbers. Parameters β and Xi were obtained from the optimization procedure on the reference sets of molecules [12].
Table 1 Hierarchical numbers and universal parameter β for HF and CASSCF energies
|
X (cardinal number)
|
HF
|
CASSCF
|
Universal
|
|
d (2)
|
2.08
|
2.08
|
2.08
|
|
t (3)
|
2.96
|
2.94
|
2.96
|
|
q (4)
|
3.87
|
3.87
|
3.87
|
|
p (5)
|
5.07
|
5.08
|
5.07
|
|
h (6)
|
6.12
|
6.13
|
6.13
|
|
s (7)
|
6.90
|
6.90
|
6.90
|
|
|
|
|
|
|
β
|
1.62
|
1.63
|
1.62
|
In [13, 14] a unified-single-parameter-extrapolation scheme, USPE(x), was used which assumes the form
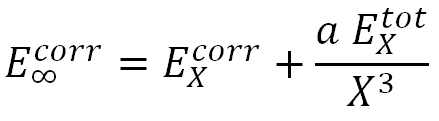
where X is a hierarchical number, and "a" is an optimized parameter obtained from the 18 molecular systems. Specifically, the values of "a" for the cc-pVXZ basis are: a = 0.0111, 0.0073, and 0.0078, respectively for MP2, CCSD and CCSD(T) and the values of "a" for the aug-cc-pVXZ basis are: a = 0.0094, 0.0061, and 0.0065, respectively for MP2, CCSD and CCSD(T).
Table below shows the hierarchical x-numbers obtained for the cc-pVXZ, XZP [15, 16] and X-ZaP [17] basis sets. As for the aug-cc-pVXZ basis set the universal x-numbers can be used [14].
| cc-pVxZ | xZP | x-LaP | Universal | |
|---|---|---|---|---|
| MP2 | ||||
| d | 2.13 |
2.13 |
2.15 |
2.13 |
| t | 2.90 |
2.90 |
2.92 |
2.90 |
| q | 3.78 |
3.83 |
3.79 |
3.78 |
| p | 4.74 |
4.74 |
4.74 |
4.74 |
| h | 5.72 |
5.72 |
5.72 |
5.72 |
| CC-Type | ||||
| d | 1.91 |
1.91 |
1.92 |
1.91 |
| t | 2.71 |
2.71 |
2.71 |
2.71 |
| q | 3.68 |
3.73 |
3.68 |
3.68 |
| p | 4.71 |
4.71 |
4.71 |
4.71 |
| h | 5.70 |
5.70 |
5.70 |
5.70 |
Disclaimer: The information contained in this website is provided in the hope that it will be useful, but WITHOUT ANY WARRANTY; without even the implied warranty of MERCHANTABILITY or FITNESS FOR A PARTICULAR PURPOSE. See the GNU General Public License for more details. By using our website, you hereby consent to our disclaimer and agree to its terms.
If you found this site useful for your work please cite it as Vladislav Vasilyev, Online complete basis set limit extrapolation calculator, Computational and Theoretical Chemistry 1115 (2017) 1–3. http://dx.doi.org/10.1016/j.comptc.2017.06.001