A mechanism of the chemical reaction describes in detail exactly what takes place at each stage of an overall chemical reaction (transformation). It also describes which bonds are broken (and in what order), and which bonds are formed (and in what order) as well as it describes structures and energies of the unstable or metastable reaction intermediates and transition states. The Transition State is usually defined as a structure along the reaction coordinate which corresponds to the highest potential energy along this coordinate.
| Figure 1. Reaction coordinate diagram for the bimolecular nucleophilic substitution (SN2) reaction between bromomethane and the hydroxide anion [Wikipedia: Transition state theory] |
In terms of Mathematics a Transition State structure of the chemical reaction represents a Saddle Point on the Potential Energy Surface (PES):
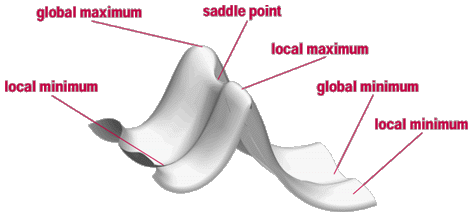 |
| Figure. An idealized Potential Energy Surface (PES) |
At both Minima and Saddle Points, the First Derivative of the energy, known as the Gradient, is zero. Since the gradient is the negative of the forces, the forces are also zero at such points. A point on the potential energy surface where the forces are zero is called a Stationary Point, with all successful optimizations locating a stationary point.
A Geometry Optimization alone of the molecular structure cannot tell you about the nature of the Stationary Point that it finds. In order to characterize a Stationary Point, it is necessary to perform a Frequency Calculation on the optimized geometry. Many Quantum Chemistry programs like Gaussian , Gamess, etc. are able to carry out such calculations.
The number of Imaginary Frequencies indicates the sort of Stationary Point to which the given molecular structure corresponds. (The Frequency values which are less than zero are known as Imaginary Frequencies.) By definition, a structure which has n imaginary frequencies is an nth order Saddle Point. Thus, the Minimum will have Zero Imaginary Frequencies, and an ordinary Transition Structure will have One Imaginary Frequency since it is a first order saddle point.
In these tutorials we shall focus on using a Gaussian programs for finding the Transition States of Chemical Reactions and how to distinguish between Minima and Saddle Points via Frequency Calculations.